Understanding Entropy for Machine Learning (December 2025 Guide)

You've probably tried calculating entropy manually and realized how tedious it gets with large datasets, especially when you're dealing with complex machine learning algorithms that rely on these measurements. Whether you're building decision trees, training neural networks, or implementing feature selection algorithms, entropy calculations can quickly become a computational bottleneck that slows down your entire workflow. Fortunately, modern tools and cloud systems make it possible to scale these calculations well, and understanding the right implementation strategies can change your approach to entropy in machine learning. With the proper foundation and computational resources, you'll be able to use entropy's full potential across all your AI projects.
TLDR:
- Shannon entropy measures uncertainty in data using H(X) = -Σ p(x) log₂(p(x)), with higher values indicating more unpredictable outcomes
- Decision trees use information gain to select optimal splits, reducing entropy at each node for better classification accuracy
- Cross-entropy loss functions guide neural network training by penalizing confident wrong predictions exponentially more than uncertain ones
- GPU acceleration reduces entropy calculation time from hours to minutes for large datasets and complex model training
- Thunder Compute provides cost savings on GPU instances with one-click deployment for entropy-based machine learning workflows
Shannon Entropy Fundamentals
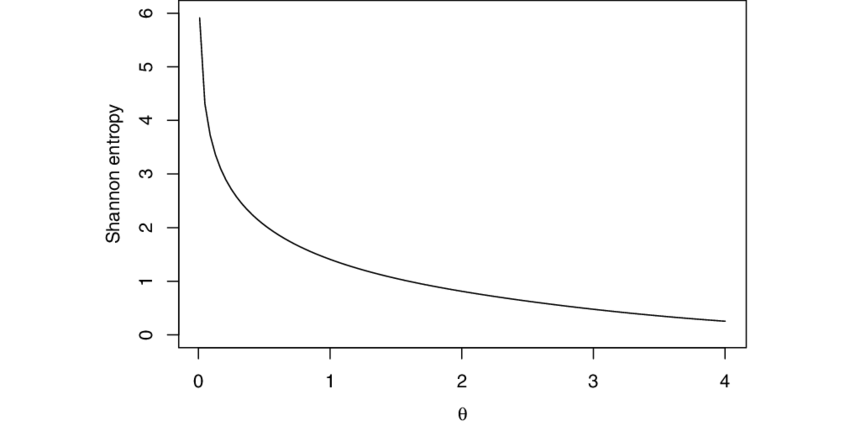
Shannon entropy stands as the cornerstone of information theory, fundamentally changing how we measure uncertainty and information content in data. Claude Shannon's 1948 paper introduced this new concept that quantifies the average level of uncertainty associated with a variable's potential states.
At its core, entropy measures uncertainty in datasets by calculating how much information each observation provides. When all outcomes are equally likely, entropy reaches its maximum value. When one outcome dominates, entropy approaches zero. Shannon entropy provides the mathematical foundation for measuring information content, making it required for machine learning algorithms that need to assess data quality and make optimal decisions.
Think of entropy as a measure of surprise. A fair coin flip has high entropy because both outcomes are equally probable. A loaded coin that lands heads 99% of the time has low entropy because the outcome is predictable.
In machine learning, entropy drives critical decisions in algorithms like decision trees, where it determines the best features for splitting data. It also powers loss functions in neural networks and helps assess model performance across classification tasks.
The beauty of Shannon entropy lies in its universal applicability. Whether you're building decision trees, training neural networks, or implementing supervised fine-tuning workflows, entropy provides the mathematical way to quantify information and uncertainty in your data.
The Shannon Entropy Formula Explained
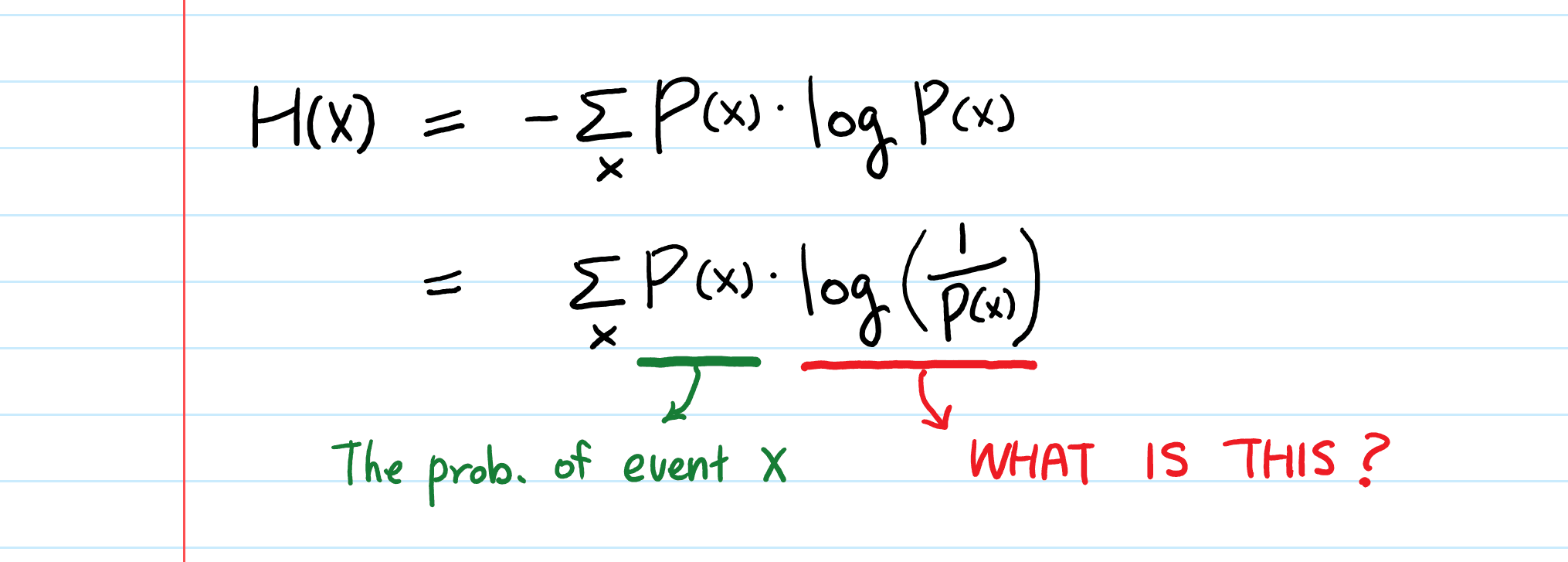
The Shannon entropy formula H(X) = -Σ p(x) log₂(p(x)) captures the essence of information measurement through its elegant mathematical structure. Each component serves a specific purpose in quantifying uncertainty:
- X is a discrete random variable
- p(x) is the probability of outcome x
- the logarithm is base 2 (when measuring information in bits).
The probability p(x) shows how likely each outcome is within your dataset. The logarithm log₂(p(x)) changes these probabilities into information units, while the negative sign keeps entropy values positive since log₂(p(x)) is negative for probabilities less than 1.
Base 2 logarithms are commonly used because they produce results measured in bits, making entropy values intuitive to interpret. Each bit equals a single binary decision's worth of information.
| Probability | -log2(p) | Surprise Level |
|---|---|---|
| 1.0 | 0 | No surprise |
| 0.5 | 1 | Medium |
| 0.25 | 2 | High |
| 0.1 | 3.32 | Very high |
The table reveals why rare events carry more information. When probability drops to 0.1, the surprise level jumps to 3.32 bits, indicating that observing this outcome provides substantial information about the system. The logarithmic relationship means that combining independent events results in additive information content, making entropy calculations mathematically tractable across complex datasets.
Implementing entropy calculations correctly requires careful consideration of edge cases, particularly when probabilities approach zero. This mathematical foundation becomes important when training models that require substantial computational resources, especially for CUDA-accelerated training workflows where entropy calculations scale across thousands of data points simultaneously.
Entropy in Decision Trees and Information Gain
Decision trees use entropy as their fundamental splitting criterion, using information gain calculations to determine optimal feature splits at each node. Information gain measures entropy reduction when changing datasets through feature-based partitions.
The information gain formula IG(S,A) = H(S) - Σ(|Sv|/|S|) × H(Sv) compares parent node entropy H(S) against weighted child node entropies. Higher information gain indicates better splits that create more homogeneous child nodes.
Consider a dataset with 8 positive and 6 negative examples. Parent entropy equals 0.985 bits. If splitting on feature A creates child nodes with entropies 0.811 and 0.592, the weighted average becomes 0.721 bits, yielding information gain of 0.264 bits.
The ID3 algorithm selects features with maximum information gain at each step. This greedy approach builds trees that minimize uncertainty at every decision point, creating more accurate classification boundaries. Information gain directly connects with feature importance in tree-based models. Features that consistently provide high information gain across multiple nodes become the most influential predictors in your model.
The recursive splitting process continues until entropy reaches acceptable thresholds or stopping criteria are met. Each split reduces overall dataset uncertainty, progressively creating purer leaf nodes that improve prediction accuracy.
Cross Entropy Loss Functions in Neural Networks
Cross entropy loss functions serve as the backbone of neural network training for classification tasks, providing mathematically sound methods for measuring prediction accuracy and guiding gradient descent optimization.
Binary Cross Entropy
Binary Cross-Entropy (BCE) is defined as: BCE = -1/N Σ[yi log(pi) + (1-yi) log(1-pi)], where yi represents true labels and pi represents predicted probabilities. This formula elegantly handles both positive and negative cases through its dual-term structure.
The logarithmic penalty structure makes confident wrong predictions receive exponentially higher penalties than uncertain ones. When a model predicts 0.9 probability for a negative example, the loss jumps dramatically compared to a 0.6 prediction for the same incorrect case.
BCE connects directly to maximum likelihood estimation, making neural network outputs interpretable as probability distributions. This probabilistic foundation allows confidence intervals and uncertainty quantification in model predictions. Binary cross entropy's asymmetric penalty structure drives models toward well-calibrated probability estimates instead of just correct classifications, improving both accuracy and reliability.
Binary cross-entropy during training helps improve predictive accuracy, so the model effectively distinguishes between two classes through optimized decision boundaries.
Categorical Cross Entropy
Categorical cross entropy extends binary classification concepts to multi-class scenarios by generalizing the loss calculation across multiple probability distributions. This criterion computes the cross entropy loss between input logits and target classes.
The softmax activation function pairs naturally with categorical cross entropy because it changes raw logits into normalized probability distributions. This combination makes sure that predicted probabilities sum to 1.0 across all classes while maintaining differentiability for backpropagation.
Entropy Applications Beyond Basic Classification
Shannon entropy extends far beyond traditional classification tasks, powering sophisticated machine learning techniques that use uncertainty quantification for enhanced model performance and data understanding and can include:
- Mutual information
- Clustering and anomaly detection
- Regularization and overfitting prevention
- Generative models and active learning
- Memory optimization
- GPU acceleration
Mutual Information for Feature Selection
Mutual information measures the statistical dependence between variables using entropy calculations. It quantifies how much knowing one variable reduces uncertainty about another, making it invaluable for identifying relevant features in high-dimensional datasets.
The formula I(X;Y) = H(X) - H(X|Y) reveals how much entropy decreases when conditioning variable X on variable Y. Features with high mutual information scores provide maximum predictive power while eliminating redundant variables that add computational overhead without improving accuracy.
Entropy in Clustering and Anomaly Detection
Clustering algorithms use entropy to check partition quality and determine optimal cluster numbers. The entropy-based silhouette coefficient measures how well data points fit their assigned clusters compared to alternative groupings.
Anomaly detection uses entropy changes as indicators of unusual patterns. When dataset entropy changes unexpectedly, it signals potential outliers or system anomalies that require investigation.
Regularization and Overfitting Prevention
Modern machine learning techniques use entropy as regularization terms to prevent overfitting. Entropy regularization encourages models to maintain uncertainty instead of making overconfident predictions on limited training data. Entropy regularization balances model complexity with generalization ability, making sure that neural networks maintain appropriate uncertainty levels across diverse input distributions.
Generative Models and Active Learning
Probabilistic models use entropy extensively to characterize and manage uncertainty in generative tasks. Variational autoencoders use entropy in their loss functions to balance reconstruction accuracy with latent space regularization. Active learning strategies select training examples based on prediction entropy, focusing annotation efforts on samples where models express highest uncertainty. This approach maximizes information gain per labeled example.
During local AI model deployment, advanced entropy implementations should prevent log(0) errors to maintain mathematical accuracy. Catastrophic cancellation occurs when subtracting nearly equal floating-point numbers during entropy summations. Using higher precision arithmetic or reformulating calculations can mitigate these stability issues in production environments.
Memory Optimization for Large Datasets
Streaming entropy calculations processes data in chunks instead of loading entire datasets into memory. This approach allows entropy computation on datasets exceeding available RAM while maintaining computational speed.
Sparse data structures reduce memory footprint when working with categorical variables containing many unique values. Hash-based probability counting eliminates the need to store explicit probability arrays for high-cardinality features. Vectorized operations using NumPy or CuPy can accelerate entropy calculations by 10-100x compared to pure Python loops, especially when processing millions of data points simultaneously.
GPU Acceleration Strategies
Modern entropy implementations use GPU parallelization to handle massive datasets efficiently. CUDA-optimized libraries like CuPy provide drop-in replacements for NumPy functions that automatically use GPU cores for parallel computation.
Thunder Compute for Entropy-Based Machine Learning
Entropy-based machine learning workflows demand major computational resources, especially when processing large datasets or training complex models. Thunder Compute provides the GPU infrastructure needed to accelerate these calculations while maintaining cost-effective performance.
Accelerating Decision Tree Training
Decision tree algorithms perform thousands of entropy calculations during training, checking potential splits across multiple features simultaneously. Thunder Compute's A100 instances allow parallel processing of these calculations, reducing training time from hours to minutes for large datasets.
Neural Network Cross-Entropy Optimization
Cross-entropy loss calculations scale linearly with batch size and class count. Thunder Compute's high-memory GPU instances handle large batch sizes well, allowing faster convergence through stable gradient estimates.
In addition, the persistent storage feature preserves model checkpoints and training state across sessions, allowing you to pause expensive training runs without losing progress. Hardware swapping lets you start development on smaller GPUs and scale to H100s for final training.
Information-Theoretic Feature Selection
Mutual information calculations require computing entropy across all feature combinations, creating computationally intensive workflows. Thunder Compute's multi-GPU instances parallelize these calculations across feature subsets, dramatically reducing selection time. The full VM control allows custom entropy implementations optimized for your specific data characteristics, while snapshots preserve configured environments for reproducible feature selection experiments across different datasets.
FAQ
How do I calculate Shannon entropy in Python for my dataset?
Use NumPy for basic calculations: probabilities = np.bincount(data) / len(data) then entropy = -np.sum(probabilities * np.log2(probabilities)). For production workflows, scipy.stats.entropy() handles edge cases automatically and provides better numerical stability.
What's the difference between Shannon entropy and cross-entropy loss?
Shannon entropy measures uncertainty in a single probability distribution, while cross-entropy loss compares two distributions (predicted vs. actual) to train neural networks. Cross-entropy loss uses Shannon entropy principles but adds prediction error penalties to guide model optimization.
When should I use information gain versus other feature selection methods?
Information gain works best for categorical features and tree-based models, providing interpretable results about feature importance. Use it when you need to understand which features reduce uncertainty most effectively, especially for decision trees and ensemble methods.
Why does my entropy calculation return NaN or infinity values?
This occurs when probabilities equal zero, causing log(0) errors. Add a small epsilon value (1e-15) to probabilities before logarithm calculations, or use scipy.stats.entropy() which handles these edge cases automatically through built-in numerical stability measures.
Can I accelerate entropy calculations for large datasets using GPUs?
Yes, GPU acceleration provides 10-100x speedups for entropy calculations on large datasets. Use CuPy for drop-in NumPy replacements that use CUDA cores, or implement custom CUDA kernels for specialized entropy workflows requiring maximum performance.
Final thoughts on mastering Shannon entropy for machine learning
Shannon entropy gives you the mathematical foundation to build smarter machine learning models, from optimizing decision trees to training neural networks with better loss functions. The computational demands of entropy calculations across large datasets make GPU acceleration important for practical implementations. Thunder Compute provides the cost-effective GPU resources you need to scale these calculations efficiently. With the right infrastructure and understanding of entropy principles, you can unlock deeper insights from your data and build more accurate predictive models.